Pergi ke kandungan

Paralaks dalam astronomi

Daripada Wikipedia, ensiklopedia bebas.
Pergerakan paralaks bintang daripada paralaks tahunan. Separuh sudut puncak ialah sudut paralaks.
Paralaks ialah sudut yang dicakup oleh garis pada suatu titik. Dalam rajah atas, Bumi dalam orbitnya menyapu sudut paralaks yang dicakup pada Matahari. Rajah bawah menunjukkan sudut yang sama disapu oleh Matahari dalam model geostatik. Rajah yang serupa boleh dilukis untuk bintang kecuali sudut paralaksnya adalah jauh lebih kecil.

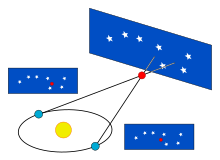
Pengukuran jarak asas yang paling penting dalam astronomi datang daripada paralaks trigonometri, seperti yang digunakan dalam kaedah paralaks bintang. Semasa Bumi mengorbit Matahari, kedudukan bintang berdekatan akan kelihatan beralih sedikit terhadap latar belakang yang lebih jauh. Anjakan ini adalah sudut dalam segi tiga sama kaki, dengan 2 AU (jarak antara kedudukan melampau orbit Bumi mengelilingi Matahari) menjadikan kaki pangkal segi tiga dan jarak ke bintang ialah kaki yang sama panjang. Jumlah anjakannya agak kecil, walaupun untuk bintang terdekat, berukuran 1 arkasaat untuk objek pada 1 jarak parsek (3.26 tahun cahaya), dan selepas itu jumlah sudut semakin berkurangan apabila jarak semakin bertambah. Ahli astronomi biasanya menyatakan jarak dalam unit parsec (parallax arcseconds; paralaks arkasaat); tahun cahaya digunakan dalam media popular.

Memandangkan paralaks menjadi lebih kecil untuk jarak bintang yang lebih besar, jarak berguna boleh diukur hanya untuk bintang yang cukup dekat untuk mempunyai paralaks lebih besar daripada beberapa kali ketepatan pengukuran. Pada tahun 1990-an, sebagai contoh, misi Hipparcos memperoleh paralaks untuk lebih seratus ribu bintang dengan ketepatan kira-kira satu miliarkasaat,[1] memberikan jarak yang berguna untuk bintang ke beberapa ratus parsek jaraknya. Kamera 3 Wide Field Teleskop Angkasa Hubble berpotensi memberikan ketepatan 20 hingga 40 mikroarkasaat, membolehkan pengukuran jarak yang boleh dipercayai sehingga 5,000 parsec (16,000 ly) untuk bilangan bintang yang kecil.[2][3] Misi angkasa Gaia memberikan jarak yang sama tepat kepada kebanyakan bintang yang lebih terang daripada magnitud ke-15. Jarak boleh diukur dalam 10% sejauh Pusat Galaksi, kira-kira 30,000 tahun cahaya jauhnya. Bintang mempunyai suatu halaju jika berbanding Matahari yang menyebabkan wujudnya gerakan wajar (melintang merentasi langit) dan halaju jejarian (gerakan ke arah atau menjauhi Matahari). Yang pertama ditentukan dengan memplotkan perubahan kedudukan bintang-bintang selama bertahun-tahun, manakala yang kedua datang daripada mengukur anjakan Doppler spektrum bintang yang disebabkan oleh gerakan di sepanjang garis penglihatan. Bagi sekumpulan bintang dengan kelas spektrum yang sama dan julat magnitud yang sama, paralaks min boleh diperoleh daripada analisis statistik pergerakan yang betul berbanding dengan halaju jejarinya. Kaedah paralaks statistik ini berguna untuk mengukur jarak bintang terang melebihi 50 parsek dan bintang pembolehubah gergasi, termasuk pembolehubah Cepheids dan pembolehubah RR Lyrae.[4]

Pengukuran paralaks mungkin merupakan petunjuk penting untuk memahami tiga komponen alam semesta yang paling sukar difahami: jirim gelap, tenaga gelap dan neutrino.[5]
Pengukuran jarak bintang ketepatan Teleskop Angkasa Hubble telah dilanjutkan 10 kali lebih jauh ke dalam Bima Sakti.[6]

Pergerakan Matahari melalui ruang angkasa menyediakan garis dasar yang lebih panjang yang akan meningkatkan ketepatan ukuran paralaks, yang dikenali sebagai paralaks sekular. Untuk bintang dalam cakera Bima Sakti pula, ini sepadan dengan garis dasar purata 4 AU setahun, manakala untuk bintang halo garis dasar ialah 40 AU setahun. Selepas beberapa dekad, garis dasar boleh menjadi susunan magnitud yang lebih besar daripada garis dasar Bumi-Matahari yang biasa digunakan untuk paralaks tradisional. Walau bagaimanapun, paralaks sekular memperkenalkan tahap ketidakpastian yang lebih tinggi kerana halaju relatif bintang yang diperhatikan adalah maklumat tambahan yang tidak diketahui. Apabila digunakan pada sampel berbilang bintang, ketidakpastian boleh dikurangkan; ketidakpastian adalah berkadar songsang dengan punca kuasa dua saiz sampel.[7]

Paralaks kelompok bergerak ialah teknik yang menggunakan pergerakan bintang individu dalam kelompok bintang berdekatan untuk mencari jarak ke gugusan. Hanya kelompok terbuka yang cukup dekat untuk teknik ini berguna. Khususnya jarak yang diperoleh untuk Hyades secara sejarahnya merupakan langkah penting dalam tangga jarak.

Objek individu lain boleh mempunyai anggaran jarak asas yang dibuat untuk mereka dalam keadaan khas. Jika pengembangan awan gas seperti sisa supernova atau nebula planet boleh diperhatikan dari semasa ke semasa, maka jarak paralaks pengembangan awan itu boleh dianggarkan. Pengukuran tersebut bagaimanapun mengalami ketidakpastian dalam sisihan objek daripada sfera. Bintang binari yang merupakan binari visual dan spektroskopik juga boleh dianggarkan jaraknya dengan cara yang sama, dan tidak mengalami ketidakpastian geometri di atas. Ciri umum kaedah ini ialah pengukuran gerakan sudut digabungkan dengan pengukuran halaju mutlak (biasanya diperoleh melalui kesan Doppler). Anggaran jarak datang daripada pengiraan sejauh mana objek mesti untuk membuat halaju mutlak yang diperhatikan kelihatan dengan gerakan sudut yang diperhatikan.

Paralaks pengembangan khususnya boleh memberikan anggaran jarak asas untuk objek yang sangat jauh, kerana pancutan supernova mempunyai halaju pengembangan yang besar dan saiz yang besar (berbanding dengan bintang). Selanjutnya, ia boleh diperhatikan dengan interferometer radio yang boleh mengukur gerakan sudut yang sangat kecil. Ini bergabung untuk memberikan anggaran jarak asas kepada supernova di galaksi lain.[8] Walaupun berharga, kes sedemikian agak jarang berlaku, jadi ia berfungsi sebagai pemeriksaan ketekalan yang penting pada tangga jarak.

Parsek

[sunting | sunting sumber]

Parsek (Jawi: ‏ڤرسيک‎‎; simbol pc) ialah unit panjang yang digunakan untuk mengukur jarak yang besar ke objek astronomi di luar Sistem Suria, lebih kurang sama dengan 3.26 light-year atau 206,265 astronomical unit (AU), iaitu 30.9 trilion kilometer (19.2 trilion Batu|batu).[a] Unit parsek diperoleh dengan menggunakan paralaks dan trigonometri, dan ditakrifkan sebagai jarak di mana 1 AU mencakupi satu arkasaat[9] (1/3600 daripada satu darjah). Bintang terdekat, Proxima Centauri, adalah kira-kira 1.3 parsec (4.2 light-year) dari Matahari: dari jarak itu, jurang antara Bumi dan Matahari menjangkau kurang sedikit daripada 1/3600 satu darjah pandangan.[10] Kebanyakan bintang yang boleh dilihat dengan mata kasar berada dalam beberapa ratus parsek dari Matahari, dengan jarak paling jauh pada beberapa ribu parsek, dan Galaksi Andromeda pada lebih 700 ribu parsek.[11]

Perkataan parsec ialah kata lakur daripada "parallax of one second (paralaks bagi satu saat lengkok)" dan dicipta oleh ahli astronomi British Herbert Hall Turner pada tahun 1913[12] untuk memudahkan pengiraan astronomi jarak astronomi daripada hanya data cerapan mentah. Memandangkan sebahagiannya atas sebab inilah unit parsek diutamakan dalam astronomi dan astrofizik, walaupun tahun cahaya kekal menonjol dalam teks sains popular dan penggunaan biasa. Walaupun parsek digunakan untuk jarak yang lebih pendek dalam Bima Sakti, gandaan parsek diperlukan untuk skala yang lebih besar di alam semesta, termasuk kiloparsek (kpc) untuk lebih banyak objek jauh di dalam dan sekitar Bima Sakti, megaparsek (Mpc) untuk galaksi jarak pertengahan, dan gigaparsek (Gpc) untuk banyak kuasar dan galaksi paling jauh.

Pada Ogos 2015, Kesatuan Astronomi Antarabangsa (IAU) meluluskan Resolusi B2 yang, sebagai sebahagian daripada takrif skala piawai mutlak dan ketara magnitud bolometrik, menyebut takrifan eksplisit sedia ada parsek sebagai tepat kepada 648000/π au, atau lebih kurang 3.0856775814913673×1016 meter (berdasarkan takrifan unit astronomi IAU 2012). Ini sepadan dengan takrifan sudut kecil parsek yang terdapat dalam banyak rujukan astronomi.[13][14]

Paralaks bintang

[sunting | sunting sumber]
Rencana utama: Paralaks bintang
Pergerakan paralaks bintang

Paralaks bintang yang dicipta oleh gerakan relatif antara Bumi dan bintang boleh dilihat, dalam model Copernicus, sebagai kesan daripada orbit Bumi mengelilingi Matahari: bintang itu hanya kelihatan bergerak jika dibandingkan kepada objek yang lebih jauh di langit. Dalam model geostatik, pergerakan bintang perlu diambil sebagai nyata dengan bintang tersebut berayun merentasi langit berbanding dengan bintang latar belakang.

Paralaks bintang paling kerap diukur menggunakan paralaks tahunan, ditakrifkan sebagai perbezaan kedudukan bintang seperti yang dilihat dari Bumi dan Matahari, iaitu sudut yang dicangkum pada bintang dengan jejari min orbit Bumi mengelilingi Matahari. Parsek (3.26 tahun cahaya) ditakrifkan sebagai jarak paralaks tahunan iaitu 1 arkasaat. Paralaks tahunan biasanya diukur dengan memerhatikan kedudukan bintang pada masa yang berbeza dalam setahun ketika Bumi bergerak melalui orbitnya. Pengukuran paralaks tahunan ialah cara pertama yang boleh dipercayai untuk menentukan jarak ke bintang terdekat. Pengukuran pertama paralaks bintang yang berjaya dibuat oleh Friedrich Bessel pada tahun 1838 untuk bintang 61 Cygni menggunakan heliometer.[15] Paralaks bintang kekal sebagai piawaian untuk menentukur kaedah pengukuran lain. Pengiraan jarak yang tepat berdasarkan paralaks bintang memerlukan ukuran jarak dari Bumi ke Matahari, kini berdasarkan pantulan radar dari permukaan planet-planet.[16]

Sudut yang terlibat dalam pengiraan ini adalah sangat kecil dan dengan itu sukar untuk diukur. Bintang terdekat dengan Matahari (dan dengan itu bintang dengan paralaks terbesar), Proxima Centauri, mempunyai paralaks 0.7687 ± 0.0003 arkasaat.[17] Sudut ini adalah anggaran yang dicakup oleh objek berdiameter 2 sentimeter yang terletak 5.3 kilometer jauhnya.

Teleskop Angkasa Hubble – Pengimbasan ruang mengukur jarak sehingga 10,000 tahun cahaya dengan tepat (10 April 2014).[18]

Hakikat bahawa paralaks bintang adalah sangat kecil sehingga ia tidak dapat diperhatikan pada masa itu digunakan sebagai hujah saintifik utama menentang heliosentrisme semasa zaman moden awal. Jelas daripada geometri Euclid bahawa kesannya tidak dapat dikesan jika bintang-bintang berada cukup jauh, tetapi atas pelbagai sebab jarak gergasi yang terlibat kelihatan tidak masuk akal: ia adalah salah satu bantahan utama Tycho terhadap heliosentrisme Copernicus yang membolehkannya serasi dengan ketiadaan paralaks bintang yang boleh dilihat, yag menganggapnya mesti ada kekosongan yang besar dan mustahil antara orbit Zuhal (ketika itu diketahui sebagai planet yang paling jauh) dan sfera kelapan (bintang tetap).[19]

Pada tahun 1989, satelit Hipparcos telah dilancarkan terutamanya untuk mendapatkan paralaks dan gerakan wajar yang lebih baik untuk lebih 100,000 bintang berdekatan, meningkatkan jangkauan kaedah sepuluh kali ganda. Walaupun begitu, Hipparcos hanya mampu mengukur sudut paralaks untuk bintang sehingga kira-kira 1,600 tahun cahaya jauhnya, lebih sedikit daripada satu peratus diameter Galaksi Bima Sakti. Misi Gaia Agensi Angkasa Eropah, yang dilancarkan pada Disember 2013, boleh mengukur sudut paralaks kepada ketepatan 10 mikroarkasaat, sekali gus memetakan bintang berdekatan (dan juga kebarangkalian planet) sehingga jarak puluhan ribu tahun cahaya dari Bumi.[20][21] Pada April 2014, ahli astronomi NASA melaporkan bahawa Teleskop Angkasa Hubble, dengan menggunakan pengimbasan ruang, boleh mengukur jarak sehingga 10,000 tahun cahaya dengan tepat, peningkatan sepuluh kali ganda berbanding pengukuran terdahulu.[18]

Paralaks harian

[sunting | sunting sumber]

Paralaks diurnal atau harian ialah paralaks yang berbeza-beza mengikut putaran Bumi atau dengan perbezaan lokasi di Bumi. Bulan dan pada tahap yang lebih kecil planet terestrial atau asteroid yang dilihat dari kedudukan pandangan yang berbeza di Bumi (pada satu masa tertentu) boleh muncul secara berbeza jika diletakkan pada latar belakang bintang tetap.[22][23]

Paralaks diurnal telah digunakan oleh John Flamsteed pada tahun 1672 untuk mengukur jarak ke Marikh pada lawannya dan melalui itu untuk menganggarkan unit astronomi dan saiz Sistem Suria.[24]

Paralaks bulan

[sunting | sunting sumber]

Paralaks bulan (selalunya singkatan paralaks mengufuk lunar atau paralaks mengufuk khatulistiwa bulan), ialah kes khas paralaks (diurnal): Bulan, sebagai jasad angkasa terdekat, mempunyai paralaks maksimum terbesar bagi mana-mana jasad angkasa, ada kala melebihi 1 darjah.[25]

Rajah untuk paralaks bintang boleh digunakan untuk menggambarkan paralaks bulan juga jika rajah diambil diperkecilkan dan diubah suai sedikit. Daripada 'berhampiran bintang', gantikan 'Bulan' dan berbanding mengambil bulatan di bahagian bawah rajah sebagai garis dasar untuk mewakili saiz orbit Bumi mengelilingi Matahari, ambil bulatan itu sebagai saiz sfera Bumi dan bulatannya mengelilingi permukaan bumi. Kemudian, paralaks bulan (mengufuk) berjumlah perbezaan dalam kedudukan sudut, berbanding latar belakang bintang jauh, Bulan seperti yang dilihat dari dua kedudukan pandangan yang berbeza di Bumi: salah satu kedudukan cerapan ialah tempat yang Bulan boleh dilihat terus di atas kepala pada masa tertentu (iaitu, dilihat sepanjang garis menegak dalam rajah); dan kedudukan cerapan yang lain ialah tempat yang Bulan boleh dilihat di ufuk pada masa yang sama (iaitu, dilihat sepanjang salah satu garis pepenjuru, dari kedudukan permukaan Bumi yang sepadan secara kasar dengan salah satu titik biru pada rajah diubah suai).

Paralaks bulan (mengufuk) secara alternatif boleh ditakrifkan sebagai sudut yang dicakup pada jarak Bulan dengan jejari Bumi[26][27] —sama dengan sudut p dalam rajah apabila dikecilkan dan diubah suai seperti yang dinyatakan di atas.

Paralaks mengufuk bulan pada bila-bila masa bergantung pada jarak linear Bulan dari Bumi. Jarak linear Bumi-Bulan berubah-ubah secara berterusan apabila Bulan mengikuti orbitnya yang terganggu dan anggaran elips mengelilingi Bumi. Julat variasi dalam jarak linear adalah dari kira-kira 56 hingga 63.7 jejari Bumi, sepadan dengan paralaks mendatar kira-kira satu darjah lengkok, tetapi antara kira-kira 61.4' hingga kira-kira 54'.[25] Almanak Astronomi dan penerbitan yang serupa menjadualkan paralaks mengufuk bulan dan/atau jarak linear Bulan dari Bumi secara berkala contohnya setiap hari untuk kemudahan ahli astronomi (dan pelayar cakerawala), dan kajian tentang cara koordinat ini berbeza dengan masa membentuk sebahagian daripada teori qamari.

Gambar rajah paralaks lunar harian

Paralaks juga boleh digunakan dalam membuat penentuan jarak ke Bulan.

Salah satu cara untuk menentukan paralaks bulan dari satu lokasi adalah dengan menggunakan gerhana bulan. Bayang-bayang penuh Bumi di Bulan mempunyai jejari kelengkungan yang jelas sama dengan perbezaan antara jejari ketara Bumi dan Matahari seperti yang dilihat dari Bulan. Jejari ini boleh dilihat bersamaan dengan 0.75 darjah, daripadanya (dengan jejari ketara suria 0.25 darjah) kita mendapat jejari ketara Bumi 1 darjah. Ini menghasilkan jarak Bumi-Bulan 60.27 kali jejari Bumi atau 384,399 kilometer (238,854 bt) Prosedur ini mula-mula digunakan oleh Aristarchus dari Samos[28] dan Hipparchus, dan kemudiannya dalam karya Ptolemy.[29] Rajah di sebelah kanan menunjukkan bagaimana paralaks bulan harian timbul dalam model planet geosentrik dan geostatik iaitu Bumi berada di tengah-tengah sistem planet dan tidak berputar. Ia juga menggambarkan perkara penting bahawa paralaks tidak perlu disebabkan oleh sebarang gerakan pemerhati, bertentangan dengan beberapa takrifan paralaks yang mengatakannya, tetapi mungkin timbul semata-mata daripada gerakan yang diperhatikan.

Kaedah lain ialah mengambil dua keping gambar Bulan pada masa yang sama dari dua lokasi yang berbeza di Bumi (lebih jauh, lebih baik) dan membandingkan kedudukan Bulan berbanding bintang. Dengan menggunakan orientasi Bumi, dua ukuran kedudukan tersebut, dan jarak antara dua lokasi di Bumi, jarak ke Bulan boleh ditriangulasi:

Contoh paralaks lunar: Okultasi Pleiades oleh Bulan

Ini adalah kaedah yang dirujuk oleh Jules Verne dalam novel terbitannya pada 1865 iaitu From the Earth to the Moon :

Sehingga itu, ramai orang tidak tahu bagaimana seseorang boleh mengira jarak yang memisahkan Bulan dari Bumi. Keadaan itu dieksploitasi untuk mengajar mereka bahawa jarak ini diperoleh dengan mengukur paralaks Bulan. Jika perkataan paralaks kelihatan memukau mereka, mereka diberitahu bahawa ia adalah sudut yang dicakup oleh dua garis lurus yang dilukis dari kedua-dua hujung jejari Bumi ke Bulan. Jika mereka mempunyai keraguan tentang kesempurnaan kaedah ini, mereka segera ditunjukkan bahawa bukan sahaja jarak min ini berjumlah keseluruhan dua ratus tiga puluh empat ribu tiga ratus empat puluh tujuh batu (94,330 farsakh) tetapi juga bahawa para astronomi tidak dalam ralat lebih daripada tujuh puluh batu (≈ 30 farsakh).

Paralaks suria

[sunting | sunting sumber]

Selepas Copernicus mencadangkan sistem heliosentriknya, dengan Bumi dalam pusingan mengelilingi Matahari, adalah mungkin untuk membina model keseluruhan Sistem Suria tanpa skala. Untuk memastikan skalanya, hanya perlu mengukur satu jarak dalam Sistem Suria, contohnya, jarak purata dari Bumi ke Matahari (kini dipanggil unit astronomi, atau AU). Apabila ditemui melalui triangulasi, ini dirujuk sebagai paralaks suria, perbezaan kedudukan Matahari seperti yang dilihat dari pusat Bumi dan satu titik satu jejari Bumi, iaitu, sudut yang dicangkum di Matahari dengan jejari min Bumi. Mengetahui paralaks suria dan purata jejari Bumi membolehkan seseorang mengira AU, langkah pertama dan kecil di jalan panjang untuk menentukan saiz dan umur pengembangan[30] Alam Semesta yang tercerap.

Cara primitif untuk menentukan jarak ke Matahari dalam istilah jarak ke Bulan telah pun dicadangkan oleh Aristarchus dari Samos dalam bukunya On the Sizes and Distances of the Sun and Moon. Beliau menyatakan bahawa Matahari, Bulan, dan Bumi membentuk segi tiga tepat (dengan sudut tepatnya di Bulan) pada saat suku bulan pertama atau terakhir. Beliau kemudian menganggarkan bahawa sudut Bulan–Bumi–Matahari ialah 87°. Menggunakan geometri yang betul tetapi data pemerhatian yang tidak tepat, Aristarchus menyimpulkan bahawa Matahari berada sedikit kurang daripada 20 kali lebih jauh daripada Bulan. Nilai sebenar sudut ini adalah hampir 89° 50', dan Matahari sebenarnya adalah kira-kira 390 kali lebih jauh.[28] Beliau menegaskan bahawa Bulan dan Matahari mempunyai saiz sudut ketara yang hampir sama lalu diameternya mestilah berkadaran dengan jaraknya dari Bumi. Oleh itu, beliau membuat kesimpulan bahawa Matahari adalah sekitar 20 kali lebih besar daripada Bulan; kesimpulan ini, walaupun tidak betul, ia masih mengikut logik tetapi dari datanya yang salah. Ia menunjukkan bahawa Matahari lebih besar daripada Bumi, yang boleh diambil untuk menyokong model heliosentrik.[31]

Mengukur masa transit Zuhrah untuk menentukan paralaks suria

Walaupun keputusan Aristarchus tidak betul kerana kesilapan dalam pemerhatian, ia masih berdasarkan kepada prinsip geometri paralaks yang betul, dan menjadi asas untuk anggaran saiz Sistem Suria selama hampir 2000 tahun, sehingga transit Zuhrah diperhatikan dengan betul pada tahun 1761 dan 1769.[28] Kaedah ini telah dicadangkan oleh Edmond Halley pada tahun 1716, walaupun dia tidak hidup untuk melihat hasilnya. Penggunaan transit Zuhrah kurang berjaya daripada yang diharapkan disebabkan oleh kesan penurunan hitam, tetapi anggaran yang terhasil ketika itu, 153 juta kilometer, hanya 2% di atas nilai yang diterima sekarang, 149.6 juta kilometer.

Tidak lama kemudian, Sistem Suria telah "diskalakan" menggunakan paralaks asteroid, beberapa daripadanya, seperti Eros, melintas lebih dekat ke Bumi berbanding Zuhrah. Dalam kedudukan bertentangan yang sesuai, Eros boleh mendekati Bumi dalam lingkungan 22 juta kilometer.[32] Semasa pertentangan 1900–1901, program di seluruh dunia telah dilancarkan untuk membuat pengukuran paralaks Eros untuk menentukan paralaks suria (atau jarak ke Matahari), dengan keputusan diterbitkan pada tahun 1910 oleh Arthur Hinks dari Cambridge[33] dan Charles D. Perrine dari Balai Cerap Lick, Universiti California.[34] Perrine menerbitkan laporan kemajuan pada tahun 1906[35] dan 1908.[36] Beliau mengambil 965 keping gambar dengan Pemantul Crossley dan memilih 525 keping gambar untuk pengukuran.[37] Program serupa kemudiannya dijalankan, semasa pendekatan yang lebih dekat, pada 1930–1931 oleh Harold Spencer Jones.[38] Nilai Unit Astronomi (kira-kira jarak Bumi-Matahari) yang diperolehi oleh program ini dianggap muktamad sehingga 1968, apabila radar dan kaedah paralaks dinamik mula menghasilkan ukuran yang lebih tepat.

Juga pantulan radar, baik di luar Venus (1958) dan luar asteroid, seperti Icarus, telah digunakan untuk penentuan paralaks suria. Hari ini, penggunaan pautan telemetri kapal angkasa telah menyelesaikan masalah lama ini. Nilai paralaks suria yang diterima pada masa ini ialah 8.794143 arkasaat.[39]

Paralaks kelompok bergerak

[sunting | sunting sumber]

Gugusan bintang terbuka Hyades di Taurus menjangkau sebahagian besar langit, 20 darjah, sehingga pergerakan yang betul seperti yang diperoleh daripada astrometri kelihatan bertumpu dengan sedikit ketepatan ke titik perspektif di utara Orion. Menggabungkan gerakan wajar ketara (sudut) yang diperhatikan dalam arkasaat lengkok dengan gerakan wajar sebenar (mutlak) yang juga diperhatikan seperti yang disaksikan oleh anjakan merah Doppler bagi garisan spektrum bintang, membolehkan anggaran jarak ke kelompok tersebut (151 tahun cahaya) dan ahli bintangnya dengan cara yang sama seperti menggunakan paralaks tahunan.[40]

Paralaks dinamik

[sunting | sunting sumber]
Rencana utama: Paralaks dinamik

Paralaks dinamik kadang kala juga digunakan untuk menentukan jarak ke supernova apabila muka gelombang optik letusan dilihat merambat melalui awan debu di sekeliling pada halaju sudut ketara, manakala halaju perambatan sebenar diketahui sebagai kelajuan cahaya.[41]

Paralaks spatio-temporal

[sunting | sunting sumber]

Daripada sistem penentududukan relativistik yang dipertingkatkan, paralaks spatio-temporal atau ruang-masa yang menggeneralisasikan tanggapan biasa paralaks dalam angkasa sahaja telah dibangunkan. Kemudian, medan peristiwa dalam ruang masa boleh disimpulkan secara langsung tanpa model perantaraan lenturan cahaya oleh badan besar seperti yang digunakan dalam formalisme PPN misalnya.[42]

Paralaks statistik

[sunting | sunting sumber]

Dua teknik yang berkaitan boleh digunakan untuk menentukan jarak purata bintang dengan memodelkan gerakan bintang. Kedua-duanya dirujuk sebagai paralaks statistik, atau secara individu dipanggil paralaks sekular dan paralaks statistik klasik.

Pergerakan Matahari melalui ruang angkasa menyediakan garis dasar yang lebih panjang yang akan meningkatkan ketepatan ukuran paralaks, yang dikenali sebagai paralaks sekular. Untuk bintang dalam cakera Bima Sakti, ini sepadan dengan purata garis dasar 4 AU setahun, manakala untuk bintang halo pula garis dasarnya ialah 40 AU setahun. Selepas beberapa dekad, garis dasar boleh menjadi susunan magnitud yang lebih besar daripada garis dasar Bumi-Matahari yang digunakan untuk paralaks tradisional. Walau bagaimanapun, paralaks sekular memperkenalkan tahap ketidakpastian yang lebih tinggi kerana halaju relatif bintang lain adalah maklumat tambahan yang tidak diketahui. Apabila digunakan pada sampel berbilang bintang, ketidakpastian boleh dikurangkan; ketepatan adalah berkadar songsang dengan punca kuasa dua saiz sampel.[43]

Purata paralaks dan jarak sekumpulan besar bintang boleh dianggarkan daripada halaju jejarian dan gerakan wajar. Ini dikenali sebagai paralaks statistik klasik. Pergerakan bintang dimodelkan untuk menghasilkan semula secara statistik penyebaran halaju berdasarkan jaraknya.[43][44]

Kaedah lain untuk pengukuran jarak dalam astronomi

[sunting | sunting sumber]

Dalam astronomi, istilah "paralaks" biasanya membawa maksud kaedah menganggar jarak, tidak semestinya menggunakan paralaks sebenar, seperti:

Lihat juga

[sunting | sunting sumber]

Nota

[sunting | sunting sumber]
  1. ^ Satu trilion di sini ialah skala pendek, iaitu 1012 (satu juta juta, atau bilion dalam skala panjang).

Rujukan

[sunting | sunting sumber]
  1. ^ Perryman, M. A. C. (1999). "The HIPPARCOS Catalogue". Astronomy and Astrophysics. 323: L49–L52. Bibcode:1997A&A...323L..49P. Unknown parameter |displayauthors= ignored (bantuan)
  2. ^ Harrington, J. D.; Villard, R. (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Diarkibkan daripada yang asal pada 17 February 2019. Dicapai pada 17 October 2014.
  3. ^ Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. (2014). "Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope". The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ...785..161R. doi:10.1088/0004-637X/785/2/161.
  4. ^ B., Baidyanath (2003). An Introduction to Astrophysics. PHI Learning Private Limited. ISBN 978-81-203-1121-3.
  5. ^ "Hubble finds Universe may be expanding faster than expected". Diarkibkan daripada yang asal pada 11 September 2018. Dicapai pada 3 June 2016.
  6. ^ "Hubble stretches the stellar tape measure ten times further". ESA/Hubble Images. Diarkibkan daripada yang asal pada October 30, 2017. Dicapai pada April 12, 2014.
  7. ^ Popowski, P.; Gould, A.. "Mathematics of Statistical Parallax and the Local Distance Scale". MISSING LINK. .
  8. ^ Bartel, N. (1994). "The shape, expansion rate and distance of supernova 1993J from VLBI measurements". Nature. 368 (6472): 610–613. Bibcode:1994Natur.368..610B. doi:10.1038/368610a0. Unknown parameter |displayauthors= ignored (bantuan)
  9. ^ "Cosmic Distance Scales – The Milky Way". Dicapai pada 24 September 2014.
  10. ^ Benedict, G. F.. "Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri". m/s. 380–384. http://clyde.as.utexas.edu/SpAstNEW/Papers_in_pdf/%7BBen93%7DEarlyProx.pdf. Diperolehi 11 July 2007.
  11. ^ "Farthest Stars". StarDate. University of Texas at Austin. 15 May 2021. Dicapai pada 5 September 2021.
  12. ^ Dyson, F. W. (March 1913). "The distribution in space of the stars in Carrington's Circumpolar Catalogue". Monthly Notices of the Royal Astronomical Society. 73 (5): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334. [paragraph 14, page 342] Taking the unit of distance R* to be that corresponding to a parallax of 1″·0 [… Footnote:]
    * There is need for a name for this unit of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek language can be overlooked, the word Astron might be adopted. Professor Turner suggests Parsec, which may be taken as an abbreviated form of "a distance corresponding to a parallax of one second".
  13. ^ Cox, Arthur N., penyunting (2000). Allen's Astrophysical Quantities (ed. 4th). New York: AIP Press / Springer. Bibcode:2000asqu.book.....C. ISBN 978-0387987460.
  14. ^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (ed. 2nd). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book.....B. ISBN 978-0-691-13026-2.
  15. ^ Zeilik & Gregory 1998, p. 44.
  16. ^ Zeilik & Gregory 1998, § 22-3.
  17. ^ Benedict; G. Fritz; Chappell, D.W.; Nelan, E.; Jefferys, W.H.; Van Altena, W.; Lee, J.; Cornell, D.; Shelus, P.J. (1999). "Interferometric Astrometry of Proxima Centauri and Barnard's Star Using Hubble Space Telescope Fine Guidance Sensor 3: Detection Limits for Substellar Companions". The Astronomical Journal. 118 (2): 1086–1100. arXiv:Astro-ph/9905318. Bibcode:1999AJ....118.1086B. doi:10.1086/300975. Unknown parameter |displayauthors= ignored (bantuan)
  18. ^ a b Harrington, J.D.; Villard, Ray (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Diarkibkan daripada yang asal pada 12 April 2014. Dicapai pada 11 April 2014.
  19. ^ Dobrzycki, J. (1973). Dobrzycki, Jerzy (penyunting). The Reception of Copernicus' Heliocentric Theory. m/s. 51. doi:10.1007/978-94-015-7614-7. ISBN 978-90-481-8340-1.
  20. ^ "Soyuz ST-B successfully launches Gaia space observatory". nasaspaceflight.com. 19 December 2013. Diarkibkan daripada yang asal pada 19 December 2013. Dicapai pada 19 December 2013.
  21. ^ Henney, Paul J. "ESA's Gaia Mission to study stars". Astronomy Today. Diarkibkan daripada yang asal pada 2008-03-17. Dicapai pada 2008-03-08.
  22. ^ Seidelmann, P. Kenneth (2005). Explanatory Supplement to the Astronomical Almanac. University Science Books. m/s. 123–125. ISBN 978-1-891389-45-0.
  23. ^ Barbieri, Cesare (2007). Fundamentals of astronomy. CRC Press. m/s. 132–135. ISBN 978-0-7503-0886-1.
  24. ^ Van Helden, A. (2010). Measuring the universe: cosmic dimensions from Aristarchus to Halley. University of Chicago Press. Ch. 12.
  25. ^ a b "D". The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981."D". The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981.
  26. ^ The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981. m/s. M10.
  27. ^ United States Naval Observatory. Nautical Almanac Office; Great Britain. Nautical Almanac Office (2006). Explanatory Supplement to the Astronomical Almanac. University Science Books. m/s. 125. ISBN 978-1-891389-45-0.
  28. ^ a b c Gutzwiller, Martin C. (1998). "Moon–Earth–Sun: The oldest three-body problem". Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589.
  29. ^ Webb, Stephen (1999), "3.2 Aristarchus, Hipparchus, and Ptolemy", Measuring the Universe: The Cosmological Distance Ladder, Springer, m/s. 27–35, ISBN 9781852331061. See in particular p. 33: "Almost everything we know about Hipparchus comes down to us by way of Ptolemy."
  30. ^ Freedman, W.L. (2000). "The Hubble constant and the expansion age of the Universe". Physics Reports. 333 (1): 13–31. arXiv:astro-ph/9909076. Bibcode:2000PhR...333...13F. doi:10.1016/S0370-1573(00)00013-2.
  31. ^ Al-Khalili, Jim (2010), Pathfinders: The Golden Age of Arabic Science, Penguin UK, m/s. 270, ISBN 9780141965017, diarkibkan daripada yang asal pada 2015-03-17, Some have suggested that his calculation of the relative size of the earth and sun led Aristarchus to conclude that it made more sense for the earth to be moving around the much larger sun than the other way round.
  32. ^ Whipple 2007.
  33. ^ Hinks, Arthur R. (1909). "Solar Parallax Papers No. 7: The General Solution from the Photographic Right Ascensions of Eros, at the Opposition of 1900". Monthly Notices of the Royal Astronomical Society. 69 (7): 544–67. Bibcode:1909MNRAS..69..544H. doi:10.1093/mnras/69.7.544.
  34. ^ Perrine, Charles D. (1910). Determination of the solar parallax from photographs of Eros made with the Crossley reflector of the Lick Observatory University of California (ed. First). Washington, D. C.: Carnegie Institution of Washington. m/s. 1–104.
  35. ^ Perrine, C. D. (1906). "The Measurement and Reduction of the Photographs of Eros Made With the Crossley Reflector in 1900". Publications of the Astronomical Society of the Pacific. 18 (10): 226.
  36. ^ Perrine, Charles D. (1908). "Progress on the Crossley Eros Solar Parallax Work". Publications of the Astronomical Society of the Pacific. 20 (120): 184. Bibcode:1908PASP...20..184P. doi:10.1086/121816.
  37. ^ Campbell, W. W. (1906). "Reports of the Observatories: Lick Observatory". Publications of the Astronomical Society of the Pacific. 19 (113): 92.
  38. ^ Jones, H. Spencer (1941). "The Solar Parallax and the Mass of the Moon from Observations of Eros at the Opposition of 1931". Mem. Roy. Astron. Soc. 66: 11–66.
  39. ^ "Astronomical Constants" (PDF). US Naval Observatory. Diarkibkan daripada yang asal (PDF) pada 2011-07-20.
  40. ^ Vijay K. Narayanan; Andrew Gould (1999). "A Precision Test of Hipparcos Systematics toward the Hyades". The Astrophysical Journal. 515 (1): 256. arXiv:astro-ph/9808284. Bibcode:1999ApJ...515..256N. doi:10.1086/307021.
  41. ^ Panagia, N.; Gilmozzi, R.; MacChetto, F.; Adorf, H.-M.; Kirshner, R.P. (1991). "Properties of the SN 1987A circumstellar ring and the distance to the Large Magellanic Cloud". The Astrophysical Journal. 380: L23. Bibcode:1991ApJ...380L..23P. doi:10.1086/186164. Unknown parameter |displayauthors= ignored (bantuan)
  42. ^ Rubin, J.L. (2015). "Relativistic Pentametric Coordinates from Relativistic Localizing Systems and the Projective Geometry of the Spacetime Manifold". Electronic Journal of Theoretical Physics. 12 (32): 83–112. Diarkibkan daripada yang asal pada 2015-02-08.
  43. ^ a b Popowski, Piotr; Gould, Andrew (29 January 1998). "Mathematics of Statistical Parallax and the Local Distance Scale". arXiv:astro-ph/9703140. Bibcode:1997astro.ph..3140P. Cite journal requires |journal= (bantuan)
  44. ^ Layden, Andrew C; Hanson, Robert B; Hawley, Suzanne L; Klemola, Arnold R; Hanley, Christopher J (1996). "The Absolute Magnitude and Kinematics of RR Lyrae Stars Via Statistical Parallax". The Astronomical Journal. 112: 2110. arXiv:astro-ph/9608108. Bibcode:1996AJ....112.2110L. doi:10.1086/118167.
Diambil daripada "https://ms.wikipedia.org/w/index.php?title=Paralaks_dalam_astronomi&oldid=6045125"