Ruang vektor

Penambahan vektor dan pendaraban skalar: vektor v (biru) ditambah kepada vektor w (merah, ilustrasi atas). Di bawah, w diregangkan dengan faktor 2, menghasilkan hasil tambah v + 2w.

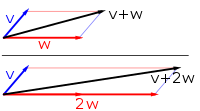
Dalam matematik, fizik dan kejuruteraan, ruang vektor (juga dipanggil ruang linear) ialah satu set objek yang dipanggil vektor, yang boleh ditambah bersama dan didarabkan ("berskala") dengan nombor yang dipanggil skalar. Skalar selalunya ialah nombor nyata, tetapi sesetengah ruang vektor mempunyai pendaraban skalar dengan nombor kompleks atau, secara amnya, dengan skalar daripada sebarang medan matematik. Operasi penambahan vektor dan pendaraban skalar mesti memenuhi keperluan tertentu, dipanggil aksiom vektor. Untuk menentukan sama ada skalar dalam ruang vektor tertentu ialah nombor nyata atau nombor kompleks, istilah ruang vektor nyata dan ruang vektor kompleks sering digunakan.

Rujukan

Algebra

• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
• Blass, Andreas (1984), "Existence of bases implies the axiom of choice", Axiomatic set theory (Boulder, Colorado, 1983) (PDF), Contemporary Mathematics, 31, Providence, R.I.: American Mathematical Society, m/s. 31–33, MR 0763890
• Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
• Templat:Lang Algebra
• Mac Lane, Saunders (1999), Algebra (ed. 3rd), m/s. 193–222, ISBN 978-0-8218-1646-2
• Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8
• Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics, 135 (ed. 2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-24766-3
• Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5
• van der Waerden, Bartel Leendert (1993), Algebra (dalam bahasa Jerman) (ed. 9th), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56799-8

Analisis

• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13627-9
• Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41129-1
• Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97894-9
• BSE-3 (2001), "Tangent plane", dalam Hazewinkel, Michiel (penyunting), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Choquet, Gustave (1966), Topology, Boston, MA: Academic Press
• Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0
• Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
• Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3
• Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9
• Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3
• Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 978-0-387-98485-8
• Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (ed. 2nd), Harlow, Essex, England: Prentice-Hall (diterbitkan 2002), ISBN 978-0-201-59619-9
• Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
• Kreyszig, Erwin (1988), Advanced Engineering Mathematics (ed. 6th), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
• Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-50459-7, MR 0992618
• Lang, Serge (1983), Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5
• Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94001-4
• Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., m/s. x+190, hdl:2027/uc1.b4250788
• Templat:Narici Beckenstein Topological Vector Spaces
• Templat:Schaefer Wolff Topological Vector Spaces
• Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press

Rujukan bersejarah

• Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (dalam bahasa Perancis), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (dalam bahasa Jerman)
• Bellavitis, Giuso (1833), "Sopra alcune applicazioni di un nuovo metodo di geometria analitica", Il poligrafo giornale di scienze, lettre ed arti, Verona, 13: 53–61.
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (dalam bahasa Perancis), Paris: Hermann
• Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR 1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (dalam bahasa Perancis), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (dalam bahasa Jerman), O. Wigand, reprint: Grassmann, Hermann (2000), Kannenberg, L.C. (penyunting), Extension Theory, diterjemahkan oleh Kannenberg, Lloyd C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
• Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (dalam bahasa Jerman), diarkibkan daripada yang asal pada 2006-11-23
• Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (dalam bahasa Itali), Turin
• Peano, G. (1901) Formulario mathematico: vct axioms via Internet Archive

Rujukan selanjutnya

• Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1
• Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (ed. 2nd), Addison-Wesley, ISBN 978-0-201-09394-0, MR 1043170
• Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64243-5
• Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1
• Coxeter, Harold Scott MacDonald (1987), Projective Geometry (ed. 2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1
• Eisenberg, Murray; Guy, Robert (1979), "A proof of the hairy ball theorem", The American Mathematical Monthly, 86 (7): 572–574, doi:10.2307/2320587, JSTOR 2320587
• Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8, MR 1322960
• Goldrei, Derek (1996), Classic Set Theory: A guided independent study (ed. 1st), London: Chapman and Hall, ISBN 978-0-412-60610-6
• Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall, ISBN 978-0-13-124405-4
• Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3
• Halpern, James D. (Jun 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society, 17 (3): 670–673, doi:10.2307/2035388, JSTOR 2035388
• Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable (ed. 6), John Wiley & Sons, ISBN 978-0470-88861-2
• Husemoller, Dale (1994), Fibre Bundles (ed. 3rd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94087-8
• Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (ed. 4th), Berlin, New York: Springer-Verlag, ISBN 978-3-540-25907-7
• Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications, m/s. xiv+352, ISBN 978-0-486-66721-8
• Kreyszig, Erwin (1999), Advanced Engineering Mathematics (ed. 8th), New York: John Wiley & Sons, ISBN 978-0-471-15496-9
• Luenberger, David (1997), Optimization by vector space methods, New York: John Wiley & Sons, ISBN 978-0-471-18117-0
• Mac Lane, Saunders (1998), Categories for the Working Mathematician (ed. 2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2
• Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
• Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9, MR 2044239
• Schönhage, A.; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)", Computing (dalam bahasa Jerman), 7 (3–4): 281–292, doi:10.1007/bf02242355, ISSN 0010-485X, S2CID 9738629
• Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
• Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6
• Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall, ISBN 978-0-13-535732-3
• Wallace, G.K. (Feb 1992), "The JPEG still picture compression standard" (PDF), IEEE Transactions on Consumer Electronics, 38 (1): xviii–xxxiv, CiteSeerX 10.1.1.318.4292, doi:10.1109/30.125072, ISSN 0098-3063, diarkibkan daripada yang asal (PDF) pada 2007-01-13, dicapai pada 2017-10-25

Pautan luar

• Hazewinkel, Michiel, penyunting (2001), "Vector space", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4