Fungsi ketumpatan kebarangkalian
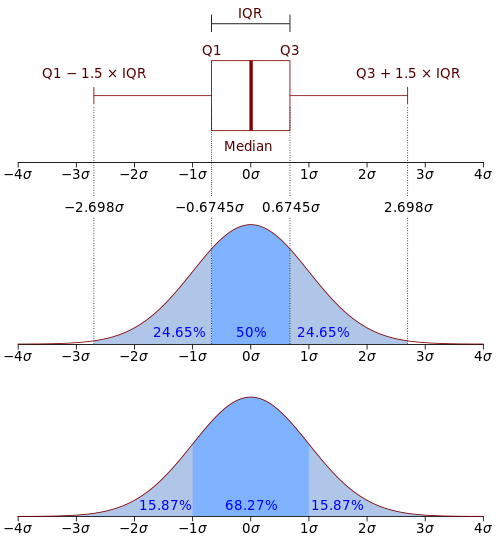

Dalam teori kebarangkalian, fungsi ketumpatan kebarangkalian (PDF), atau ketumpatan bagi pemboleh ubah rawak selanjar, ialah fungsi yang nilainya pada mana-mana sampel (atau titik) dalam ruang sampel (set kemungkinan nilai yang diambil oleh pemboleh ubah rawak) boleh ditafsirkan sebagai menyediakan kemungkinan relatif bahawa nilai pemboleh ubah rawak akan hampir dengan sampel itu.[2][3] Dalam erti kata lain, sementara kemungkinan mutlak untuk pemboleh ubah rawak berterusan untuk mengambil mana-mana nilai tertentu ialah 0 (memandangkan terdapat satu set nilai yang mungkin tidak terhingga untuk dimulakan), nilai PDF pada dua sampel berbeza boleh digunakan untuk membuat kesimpulan, dalam mana-mana cabutan tertentu pemboleh ubah rawak, berapa besar kemungkinan pemboleh ubah rawak itu akan hampir dengan satu sampel berbanding dengan sampel yang lain.
Dalam erti kata yang lebih tepat, PDF digunakan untuk menentukan kebarangkalian pemboleh ubah rawak jatuh dalam julat nilai tertentu, berbanding dengan mengambil mana-mana satu nilai. Kebarangkalian ini diberikan oleh kamiran PDF pemboleh ubah ini ke atas julat itu—iaitu, ia diberikan oleh kawasan di bawah fungsi ketumpatan tetapi di atas paksi mendatar dan antara nilai terendah dan terbesar julat. Fungsi ketumpatan kebarangkalian adalah bukan negatif di mana-mana, dan kamirannya di seluruh ruang adalah sama dengan 1.
Istilah "fungsi taburan kebarangkalian"[4] dan "fungsi kebarangkalian"[5] kadangkala juga telah digunakan untuk menunjukkan fungsi ketumpatan kebarangkalian. Walau bagaimanapun, penggunaan ini tidak piawai di kalangan ahli kebarangkalian dan statistik. Dalam sumber lain, "fungsi taburan kebarangkalian" boleh digunakan apabila taburan kebarangkalian ditakrifkan sebagai fungsi ke atas set nilai umum atau ia mungkin merujuk kepada fungsi taburan kumulatif, atau ia mungkin satu fungsi jisim kebarangkalian (PMF) dan bukannya ketumpatan. "Fungsi ketumpatan" itu sendiri juga digunakan untuk fungsi jisim kebarangkalian, yang membawa kepada kekeliruan selanjutnya.[6] Namun secara umum, PMF digunakan dalam konteks pemboleh ubah rawak diskret (pemboleh ubah rawak yang mengambil nilai pada set boleh dikira), manakala PDF digunakan dalam konteks pemboleh ubah rawak selanjar.
Rujukan
[sunting | sunting sumber]- ^ "AP Statistics Review - Density Curves and the Normal Distributions". Diarkibkan daripada yang asal pada 2 April 2015. Dicapai pada 16 March 2015.
- ^ Grinstead, Charles M.; Snell, J. Laurie (2009). "Conditional Probability - Discrete Conditional" (PDF). Grinstead & Snell's Introduction to Probability. Orange Grove Texts. ISBN 161610046X. Dicapai pada 2019-07-25.
- ^ "probability - Is a uniformly random number over the real line a valid distribution?". Cross Validated. Dicapai pada 2021-10-06.
- ^ Probability distribution function PlanetMath Diarkibkan 2011-08-07 di Wayback Machine
- ^ Probability Function di MathWorld
- ^ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (for example, Table 5.1 and Example 5.4)
Bacaan lanjut
[sunting | sunting sumber]- Billingsley, Patrick (1979). Probability and Measure. New York, Toronto, London: John Wiley and Sons. ISBN 0-471-00710-2.
- Casella, George; Berger, Roger L. (2002). Statistical Inference (ed. Second). Thomson Learning. m/s. 34–37. ISBN 0-534-24312-6.
- Stirzaker, David (2003). Elementary Probability. ISBN 0-521-42028-8. Chapters 7 to 9 are about continuous variables.
Pautan luar
[sunting | sunting sumber]- Ushakov, N.G. (2001), "Density of a probability distribution", dalam Hazewinkel, Michiel (penyunting), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Eric W. Weisstein, Fungsi ketumpatan kebarangkalian di MathWorld.
